Um cano de 1,0 cm de diâmetro se alarga para 2,0 cm e, depois, se estreita para 5,0 mm. Um líquido flui pelo primeiro segmento a uma velocidade de 4,0 m/s.
a. Qual é a velocidade no segundo e no terceiro segmento?
b. Qual é a vazão de volume no cano?
Passo 1
Bom! Temos aí uma questão sobre vazão!
Por isso, vamos fazer um esboço do nosso problema, já que a água está fluindo em um sistema onde a seção transversal muda...
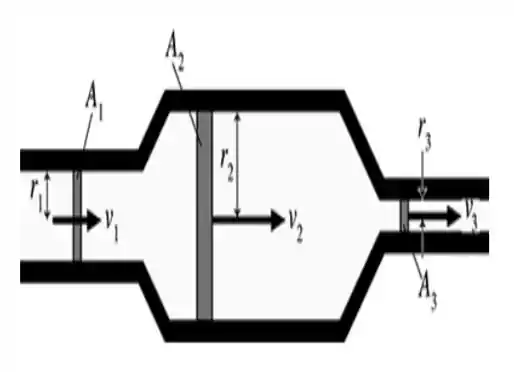
Opaaa! Acho que já temos aí uma dica de como vamos ter que resolver essa questão! Pelo visto, vamos ter que usar a famosa equação da continuidade!
Essa equação relaciona a velocidade de escoamento de um fluido e a área disponível para tal escoamento. A partir da imagem abaixo, perceba que o caminho feito pelo fluido possui duas áreas diferentes: . Imagine, portanto, que, em um intervalo de tempo (), um volume () do fluido entre pela área . Adotando o fluido como incompressível, devemos assumir que o mesmo volume () deverá sair pela extremidade da área ...

Passo 2
a) Baseado nisso, sabendo que...
Usando o Teorema da Continuidade...
Podemos obter a velocidade no segundo segmento...
E no terceiro segmento...
Passo 3
b) Por fim, falta determinar a vazão de volume no cano!
Essa é de boas!
Bom! Pela equação da continuidade, a vazão não muda... Portanto, se pegar , ou ... O resultado vai ser o mesmo!
Dessa forma, calculando :
Resposta
a)
b)