Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Termodinâmica Óptica- Ed: 2º - Capítulo 15.Exercícios e Problemas - Ex. 17

Uma esfera completamente imersa na água é amarrada ao fundo do recipiente por um barbante. A tensão no barbante corresponde a um terço do peso da esfera. Qual é a densidade da esfera?

Passo 1

Mais uma questãozinha de empuxo aí, guys!

Bom! Aqui a gente vai precisar montar a equação que rege todas as forças que agem sobre o bloco. As forças são: o peso, o empuxo e a tensão no barbante

Primeiro temos que apontar as forças. Tanto o peso quanto a tensão apontam pra baixo, enquanto o empuxo pra cima.

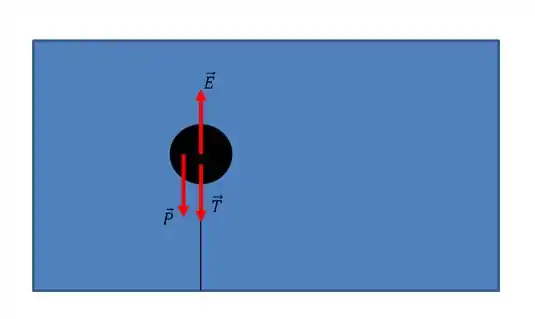
Como o bloco está em equilíbrio, a soma das forças dará zero:

E - T - P = 0

E = P + T

A tensão no barbante corresponde a um terço do peso da esfera. Logo;

T = P 3

E então, ficamos com...

E = P + P 3

E = 4 3 P

E = 4 3 m g

A massa da esfera, por sua vez, é dada pela seguinte expressão (o produto da sua densidade pelo volume):

m = ρ e s f e r a V e s f e r a

Dessa forma;

E = 4 3 ρ e s f e r a V e s f e r a g

Passo 2

O Empuxo é dado por:

E = ρ á g u a g V d e s l o c a d o

Como toda esfera está totalmente imersa em água, o volume de água deslocado por ela é o próprio volume da esfera.

V d e s l o c a d o = V e s f e r a

Sendo assim;

E = ρ á g u a V e s f e r a g

Igualando as fórmulas...

4 3 ρ e s f e r a V e s f e r a g = ρ á g u a V e s f e r a g

4 3 ρ e s f e r a = ρ á g u a

E isolando a densidade da esfera:

ρ e s f e r a = 3 4 ρ á g u a

ρ e s f e r a = 3 4 ⋅ 1000

ρ e s f e r a = 750   k g / m 3

Conseguimos obter nossa resposta!

Missão cumprida de novo!

Bora pra próxima!

Resposta

ρ e s f e r a = 750   k g / m 3

Ver Outros Exercícios desse livro