Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 30.Exercícios e Problemas - Ex. 64
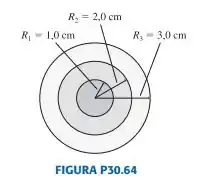
Qual é a capacitância das três cascas esféricas metálicas concêntricas da FIGURA P30.64? DICA: Você consegue conceber isso como uma combinação de capacitores?
Passo 1
Faaaaaala, galera... Tranquileba??
Como é pedido a capacitância, que por definição é:
Precisamos achar a diferença de potencial V. Como? Achando o campo eletrico no objeto. Sim! Veja:
Como achar o campo na esfera? Pela lei de Gauss, assim:
Considerando o campo eletrico constante:
Sabendo que a are ade uma esfera é:
Assim:
Assim temos o campo. Mas o enunciado nos dá informação do potencial, assim:
De modo que:
Portanto:
Tomaremos a diferença de potencial de e para calcular a capacitância.
Passo 2
Assim, para a diferença e potencial de :
De modo que:
E para :
De modo que:
Estando, segundo a imagem, ambos os capacitores em série, tomaremos a lei dos capacitores em série:
Colocando nossos valores achados:
Portanto:
Em outras palavras, a capacitância entre a capacitância interna e externa não atua na capacitância equivalente.
Passo 3
Colocando valores: