Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 30.Exercícios e Problemas - Ex. 49

A FIGURA P30.49 mostra o potencial elétrico nos pontos sobre uma grade de 5,0   c m ×   5,0   c m .

  1. Reproduza essa figura em uma folha de papel e depois desenhe as superfícies equipotenciais correspondentes a 50   V ,   75   V   e   100   V .
  2. Estime o campo elétrico (intensidade e orientação) nos pontos A, B, C e D.
  3. Desenhe os vetores do campo elétrico nos pontos A, B, C e D em seu diagrama.

Passo 1

Faaaaaala, galera... Tranquileba??

Para a)

Sabemos que as superfícies de potencias são equipotenciais, logo as superfícies pedidas são de mesma potencias, nosso trabalho é de ligar os pontos.

Fazendo já o item c)

Sabemos que:

E → = - ∇ ∙ V →

Pelo significado da gradiente nós temos que: aponta aonde a função vai crescer

Estando um símbolo negativo na frente, logo aponta contrario para onde a função cresce.

Assim, o desenho do item a com o item c é:

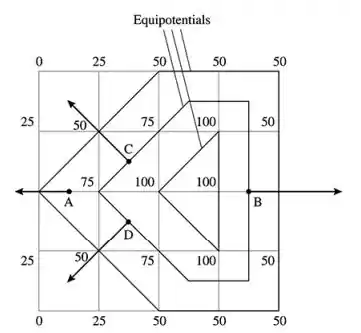
Passo 2

Para b)

Usando a equação já dada no passo anterior:

E = Δ V Δ s

Passo 3

Assim, para o ponto A o campo elétrico é:

E a = 75 V - 50 V 0.05   m = 500 V m

Para o ponto b:

E b = 100 V - 50 V 0.05 m = 1000 V m

Para c)

Tomando o ponto está na diagonal, tomemos a distancia em metro pelo teorema de pitagoras:

d = ( 5 c m 2 + 5 c m 2 = 50   c m 2 = 5 c m 2

E c = 100 V - 50 V 0.05   m 2 = 707   V

E o ângulo é de tan ⁡ θ = 5 c m 5 c m → θ = 45 ° acima, para esquerda.

E o ponto d está na mesma linha e mesma posição, logo E d = 707   V , para baixo e esquerda

Resposta

Para a e c)

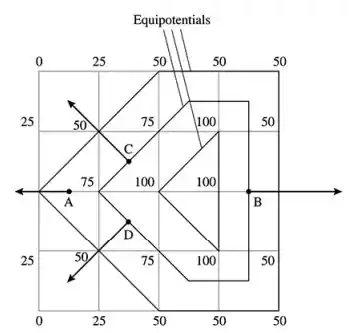
Para b)

E a = = 500 V m

E b = 1000 V m

Para c)

= 707   V

θ = 45 ° acima, para esquerda.

E d = 707   V

θ = 45 ° baixo, para esquerda.

Ver Outros Exercícios desse livro