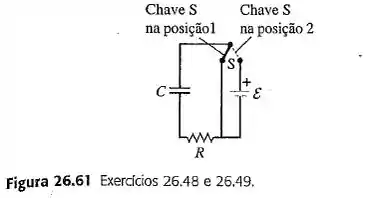
Um capacitor com é conectado em série, como indicado na Figura 26.61, a um resistor e uma fonte de fem , cuja resistencia interna é desprezivel. Inicialmente, o capacitor está descarregando e a chave S está na posição 1. A seguir, a chave S é colocada na posição 2, de modo que o capacitor começa a se carregar. Depois de permanecer na posição 2 durante 10,0 ms, a chave é colocada novamente na posição 1, de modo que o capacitor começa a se descarregar. (a) Calculque a carga do capacitor imediatamente antes de a chabe ser colocada novamente na posição 1. (b) Determine a queda de voltafem nos terminais do resistor e nos terminais do capacitor no instente mencionado no item (a). (c) Calculque a queda de voltagem nos terminais do resistor e nos terminais do capacitor imediantamente depois que a chave é retirada da posição 2 e colocada novamente naposição 1. (d) Calcule a carga do capacitor 10,0 ms depois que a chave sai da posição 2 e volta para a posição 1.
Passo 1
E ai galera, aqui para cada circuito, aplique a regra do circuito para relacionar as tensões entre os elementos do circuito.
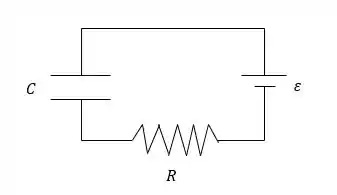
- Com o interruptor na posição , o circuito é o circuito de carga mostrado na Figura a seguir:
- E
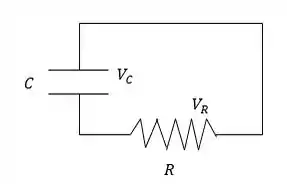
- Colocar o interruptor de volta na posição produz o circuito de descarga mostrado na Figura a seguir:
- No circuito de descarga, a carga no capacitor em função do tempo é dada pela equação
Em , .
A carga q no capacitor é dada em função do tempo pela equação:
Então, em
Passo 2
A regra do loop diz:
Passo 3
A carga inicial é a carga calculada na parte (b),
o mesmo que antes de o interruptor ser acionado. Mas agora:
, então
Passo 4
Que implica:
o mesmo que na parte (a). Assim, em
Passo 2
é menor que uma constante de tempo; portanto, no instante descrito na parte (a), o capacitor não está completamente carregado; sua tensão é menor que a fem. Existe uma corrente de carga e uma queda de tensão no resistor. No circuito de descarga, a tensão no capacitor começa em e diminui. Após diminuiu para: