Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 30.Exercícios e Problemas - Ex. 83

A carga está uniformemente distribuída, com densidade de carga ρ , em um cilindro muito comprido e de raio R. Encontre a diferença de potencial entre a superfície e o eixo do cilindro

Passo 1

Faaaaaala, galera... Tranquileba??

Sabemos que:

E → = - ∇   V →   → V → = - ∮ E → d s                   ( 0.1 )

Então para um campo uniforme e simétrico, fica mais fácil se nós acharmos o campo, que é facilmente achado pela Lei de Gauss para o fluxo elétrico e assim achar o potencial.

Lei de Gauss:

∮ E * d A = Q i n t ε 0                       ( 0.2 )

E uma representação do enunciado:

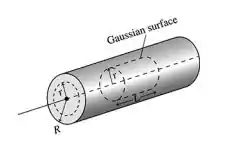
Passo 2

Assim:

∮ E * d A = E * A = Q i n t ε 0                        

Seja a área de um cilindro A = 2 π r L

E sabemos que, para o volume, a densidade de carga volumétrica é:

ρ = Q V → Q = ρ V

E o volume de um cilindro é V = π r 2 L .

Assim:

E * A = Q i n t ε 0 → = E * 2 π r   L = ρ π r 2 L ε

Logo:

E = ρ 2 ε 0   r

Passo 3

Assim, fazendo uso da equação (0.1):

Δ V = ∮ E * d s

Sendo d s → c a m i n h o . Nesse caso o caminho é em d r . E claro, 0 que é o ponto da carga, até o R do cilindro. Assim:

Δ V = - ∮ 0 R ρ 2 ε o r d r

Δ V = - ρ 2 ε 0 R 2 2 = - ρ R 2 4 ε 0

Resposta

Δ V = - ρ R 2 4 ε 0

Ver Outros Exercícios desse livro