Enunciado
Física - Halliday - Vol 3- Ed: 8º - Capítulo 21.4 - Ex. 15ab
As cargas e coordenadas de duas partículas mantidas fixas no plano são , , e , , . Determine (a) o módulo e (b) a orientação da força eletrostática que a partícula exerce sobre a partícula . Determine também ( c) a coordenada x e ( d) a coordenada y de uma terceira partícula de carga para que a força exercida sobre a partícula pelas partículas e seja nula.
Passo 1
Faaaaaala galerinha, bora começar?
Antes de qualquer coisa vamos desenhar as cargas, tudo bem?
Vamos começar achando a distância entre as cargas 1 e 2, porque iremos precisar dela, ok?
Se vocês olharem bem o desenho acima irão observar que a distância entre elas, d, é também a hipotenusa de um triângulo retângulo:
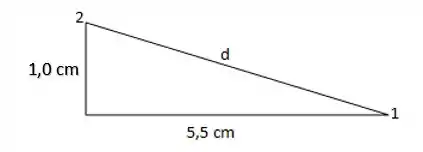
Então:
Para calcular as forças eletrostáticas usamos a Lei Coulomb, certo?
Bora relembrar?
Sabemos que:
Vamos substituir?
Passo 2
Achamos a letra (a), mas ainda precisamos a sua orientação, certo?
Vamos olhar novamente para o triângulo retângulo formado, e o ângulo que a força faz com a horizontal:
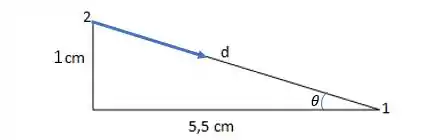
Para achar o ângulo vamos usar a tangente:
Se formos colocar a orientação em relação ao ângulo que a força faz com o eixo positivo, teríamos que esse ângulo seria igual a , porque a força está a baixo do eixo positivo.
Isso porque?
Porque as cargas têm sinais opostos!! Então a força que ocorre entre elas é de atração! No desenho:
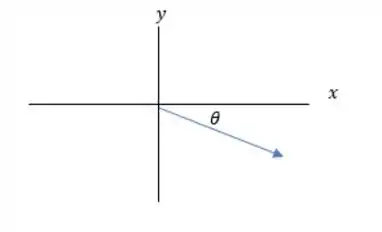
Sacou?
Vamos seguindo?