Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Campos e Ondas- Ed: 2º - Capítulo 14.Problemas - Ex. 30

Para as cargas no Problema 14.29, suponha que uma partícula carregada positivamente de carga q’ e massa m é deslocado ligeiramente da origem na direção do eixo x e, em seguida, lançado. (a) Qual é a sua velocidade no infinito? (b) Esboce um gráfico da velocidade da partícula em função de x

Passo 1

E ai gente, beleza?

Vem comigo fazer essa questão aqui!

Letra a:

Aplicando a lei da conservação de energia:

1 2 m v 2 + c y 0 = 1 2 m v 1 2 + q v ∞

Então,

q v 0 = 1 2 m v 1 2 → v 1 2 = 2 g V 0 m                               1

v 1 2 = 2 q m × q 2 π ε 0 a → V 1 2 = q 2 m r ϵ 0 a

v 1 = q m π ε a a 1 / 2

Tendo em conta que a partícula se move da origem, então sua velocidade no infinito é:

v 1 2 = 2 q m × 2 q 4 π ε 0 x 2 + a 2 → v 1 2 = q 2 π ε 0 m x 2 + a 2

v 1 = q π ϵ 0 m 1 2 × x 2 + a 2 1 4

Passo 2

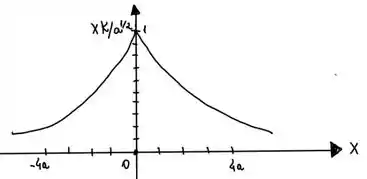
Letra b:

Como k = q π ϵ m 1 2 , então o gráfico é:

Passo 3

  1. v 1 = q π ϵ 0 m 1 2 × x 2 + a 2 1 4
  2. Ver gráfico

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro