Um ciclista está descendo em linha reta uma colina a uma velocidade constante. A massa combinada do ciclista e da bicicleta é de 80,0 kg, e o morro tem uma inclinação de 15,0 em relação à horizontal. A resistência do ar opõe-se ao movimento do ciclista. Mais tarde, o ciclista sobe a mesma colina na mesma velocidade constante. Quanta força (dirigida paralelamente à colina) deve ser aplicada à bicicleta para que o ciclista possa subir a colina?

Quando a bicicleta está descendo a encosta, as forças que agem sobre ele são a força normal () exercido pela superfície da colina, a força da gravidade , e a força da resistência do ar .

Quando a bicicleta sobe o morro, tem uma força adicional; é a força aplicada que é necessária para o ciclista subir a colina em velocidade constante. Podemos usar nosso conhecimento do movimento da bicicleta colina abaixo para encontrar . Uma vez que é conhecido, podemos analisar o movimento da bicicleta conforme ela sobe a colina.

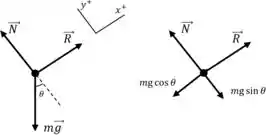
Vamos fazer o diagrama de corpo livre para as forças durante o movimento em declive (na esquerda).

A colina está inclinada em um ângulo acima da horizontal.

Outro diagrama (na direita) também mostra essas forças resolvidas em componentes paralelos e perpendicular à linha de movimento.

Como a bicicleta tá com uma velocidade constante, a aceleração é zero. Então, de acordo com a segunda lei de Newton, temos o equilíbrio das forças. Fazendo o equilíbrio das forças no eixo :

Quando o ciclista sobe a mesma colina em velocidade constante, uma força aplicada deve empurrar o sistema subindo a colina.

Como a velocidade é a mesma, a magnitude da força da resistência do ar permanecerá igual ().

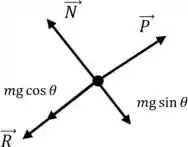
No entanto, a resistência do ar irá vai estar ao contrário do movimento, apontando para baixo da colina. A figura abaixo mostra as forças que atuam no sistema durante o movimento ascendente. Usando a mesma convenção de sinais que usamos, temos

Fazendo o equilíbrio de forças na direção do eixo :