Um cilindro de de altura flutua na água com seu eixo perpendicular à superfície. O comprimento do cilindro acima da água é de . Qual é a densidade do cilindro?
Passo 1
Bom, galera, aqui a gente vai precisar montar a equação que rege todas as forças que agem sobre o cilindro.
Por isso, vamos fazer um diagrama de corpo livre pra ele...
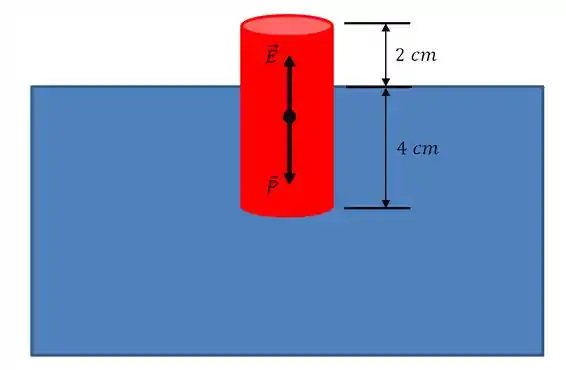
As forças no caso aí são: o peso e o empuxo
Primeiro temos que apontar as forças. O empuxo aponta pra cima, enquanto o peso pra baixo.
Como o bloco está em equilíbrio, a soma das forças dará zero:
Vamos calcular essas duas forças!
O peso é dado por:
Onde a massa do cilindro, , é dada por...
Sendo é a área da seção transversal do cilindro!
Não precisa se preocupar com esse , porque mais pra frente cê vai entender que no final das contas ele nem vai fazer diferença!
Passo 2
O Empuxo é dado por:
Como apenas do cilindro estão imersos na água, o volume de água deslocado vai ser igual à...
Com
Dessa forma, igualando com :
Viu só! O acabou sendo cortado em ambos os lados! Nem fez diferença!
Isolando a densidade do cilindro...
Ao substituir os valores numéricos...
Conseguimos achar a densidade do cilindro!
Pronto! Terminamos aqui!
Missão cumprida!