Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 31.Exercícios e Problemas - Ex. 51
Um cilindro de metal oco tem um raio interno a, um raio externo b, comprimento L e condutividade . A corrente é radial e aponta para fora, da superfície interna para a externa.
- Obtenha uma expressão para a intensidade de campo elétrico no interior do metal em função do raio r medido a partir do eixo do cilindro.
- Calcule a intensidade do campo elétrico nas superfícies interna e externa de um cilindro de ferro se , , e .
Passo 1
Faaaaaala, galera... Tranquileba??
Fazendo um desenho como esboço da figurada dada no enunciado, temos:
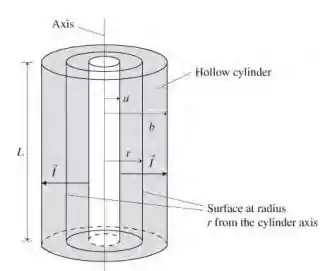
Para a)
Sabemos que:
Pede-se , assim:
E tendo a condutividade do metal como
Passo 2
Para b)
Para o campo interno (com raio a):
Passo 3
Para o campo externo (com raio b):
Resposta
Para a)
Para b)
Para o campo interno (com raio a):
Para o campo externo (com raio b):