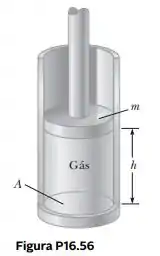
Um cilindro vertical de área transversal A é adaptado com um pistão bem ajustado, sem atrito, de massa m (Fig. P16.56). O pistão não tem seu movimento restrito de qualquer maneira e é suportado pelo gás à pressão P abaixo dele. A pressão atmosférica é . Queremos determinar a altura h na Figura P16.56. (a) Que modelo de análise é adequado para descrever o pistão? (b) Escreva uma equação de força adequada para o pistão a partir deste modelo de análise em termos de , , , e . (c) Suponha que n mols de um gás ideal estejam no cilindro a uma temperatura de . Substitua em sua resposta para a parte (b) para encontrar a altura h do pistão acima do fundo do cilindro.

As forças que atuam no pistão são a força da gravidade e a força da pressão atmosférica para baixo e a força da pressão do ar abaixo do pistão agindo para cima, e como está em equilíbrio:

Temos:

Substituindo:

Usando a lei dos gases ideais:

Substituindo:

Podemos escrever o volume:

Então:

Isolando :

Multiplicando tudo por :

Mandamos bem nessa!!!!!!

Até a próxima questão..............