Para o circuito da FIGURA P32.64, quanto valem (a) a corrente através do resistor de 2 , (b) a potência dissipada no resistor de 2 e (c) o potencial no ponto a?
Passo 1
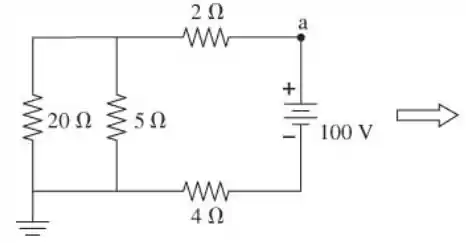
- A potência dissipada pelo resistor de 20 Ω é I 20 2 ( 20 Ω ) = ( 2,0 A ) ( 20 Ω ) = 80 W .
- Começando com potencial zero no ponto aterrado, viajamos ao longo do caminho externo para o ponto a e adicionamos/subtraímos as diferenças potenciais no caminho:
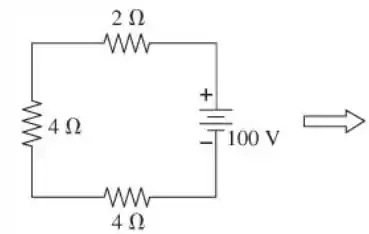
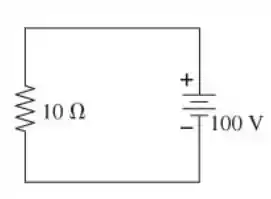
A figura mostra como simplificar o circuito da Figura P32.64 usando as leis das resistências em série e em paralelo. Tendo reduzido o circuito a uma única resistência equivalente, reverteremos o procedimento e “construímos” o circuito para encontrar a diferença de corrente e potencial de cada resistor.
a) Do último circuito da figura e da lei de Kirchhoff, I = 100 V 10 Ω = 10 A. Assim, a corrente através da bateria é de 10 A. Agora, enquanto reconstruímos o circuito, notamos que os resistores em série devem ter a mesma corrente I e que os resistores paralelos devem ter a mesma diferença de potencial.
Passo 2
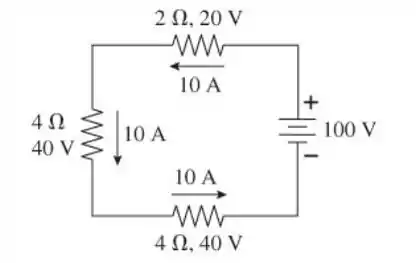
Na Etapa 1 do diagrama acima, retornamos o resistor de 10 Ω aos resistores de 4 Ω, 4 Ω e 2 Ω em série. Esses os resistores devem ter a mesma corrente de 10 A que a resistência de 10 Ω. Ou seja, a corrente através dos 2 Ω e 4 Ω resistores é de 10 A. As diferenças de potencial são
ΔV 2 = (10 A)(2 Ω ) = 20 V
ΔV 4 (esquerda) = (10 A)(4 Ω ) = 40 V
ΔV 4 (esquerda) = (10 A)(4 Ω ) = 40 V
Na Etapa 2, retornaremos o resistor de 4 Ω esquerdo para os resistores de 20 Ω e 5 Ω em paralelo. Os dois resistores devem ter a mesma diferença de potencial ΔV = 40 V. Da lei de Ohm,
As correntes através dos vários resistores são
Resposta
Ver o desenvolvimento