Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 29.Exercícios - Ex. 35

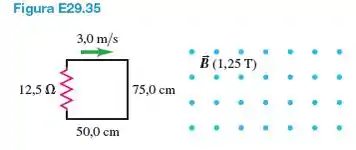
Um circuito retangular se move a uma velocidade constante de 3,0   m / s para dentro, através e para fora de um campo magnético uniforme de 1,25   T , como indica a Figura E29.35.

A região do campo magnético é consideravelmente maior que 50,0   c m . Ache o módulo e o sentido (horário ou anti-horário) da corrente induzida no circuito enquanto ele

(a) entra no campo magnético;

(b) está totalmente dentro do campo, porém ainda se movendo; e

(c) movendo-se para fora do campo.

(d) Desenhe um gráfico da corrente nesse circuito em função do tempo, incluindo os três casos anteriores.

Passo 1

Olá, tudo bem? Vou ajudar você aqui!

Letra (a):

A diferença de potencial é

ϵ = R i = B v L

i = B v L R = 1,25.3 . 0,75 12,5 = 0,225 A

Quando entra o fluxo aumenta, portanto surge um campo induzido na direção ⊗ , cuja corrente tem sentido horário.

Passo 2

Letra (b):

Nessa situação não há variação de fluxo e assim não há corrente induzida.

Passo 3

Letra (c):

Nessa situação o fluxo diminui, então temos a situação oposta da letra (a). Então aqui a corrente induzida é no sentido anti-horário e de valor igual a 0,225 A .

Resposta

a ) 0,225 A ,   h o r á r i o

b ) n ã o   h á   c o r r e n t e

c ) 0,225 A ,   a n t i - h o r á r i o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma espira quadrada é mantida em um campo magnético uniforme de 0,24 T perpendicular ao plano da espira. O comprimento dos lados do quadrado está diminuindo a uma taxa constante de 5,0 cm/s. Qual é a
Uma espira retangular de lados a e b afasta-se com velocidade v = vx ^ de um fio retilíneo muito longo, que transporta corrente contínua de intensidade I . A espira tem resistência R e autoindutância
Uma espira retangular de lados a e b de resistência R cai num plano vertical e atravessa uma camada onde existe um campo B uniforme horizontal (fig.).Repita o cálculo num instante posterior, em que a
Uma espira circular de raio a tem no seu centro uma outra espira de raio b ≪ a . Os planos das duas espiras formam entre si um ângulo θ . Calcule a indutância mútua entre elas.
Uma barra metálica com 0,360 m é puxada para a esquerda por uma força aplicada F. A barra desliza sobre trilhos metálicos paralelos conectados através de um resistor de 45,0 V, como indica a Figura E2