Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 9.Problemas - Ex. 11b
Uma espira retangular de lados e b de resistência R cai num plano vertical e atravessa uma camada onde existe um campo uniforme horizontal (fig.).
- Repita o cálculo num instante posterior, em que a espira ainda está saindo do campo e sua velocidade é .
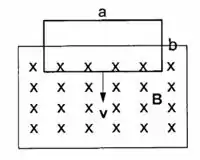
Passo 1
Se liga! Lembra que a força magnética é
Podemos achar a corrente lembrando que
Passo 2
Sabendo que o fluxo é dado por
onde o campo B é uniforme e a área S quando a espira entra no campo é dada por
Assim podemos escrever que
Agora vamos achar a corrente
Se liga que, como temos que a área está diminuindo, a variação do campo fluxo será negativa, sendo assim a corrente estará indo no sentido horário.
Lembra que , logo
Passo 3
Retornando para a equação da força, teremos
Resposta
Exercícios de Livros Relacionados
O campo magnético B → em todos os pontos de uma região circular de raio R é uniforme e está direcionado para o interior do plano da página, como indicado na figura 29.54. (Essa região poderia ser a se
Calcule a auto-indutância de uma bobina toroidal de secção quadrada com lado L e de raio médio R .
51- Como novo engenheiro elétrico da companhia elétrica local, você é designado para projetar um gerador de voltagem senoidal C A com voltagem máxima de 120V . Além de muito fio, você recebe dois ímãs
44- Variação no campo magnético. Você está testando um novo sistema de captura de dados. Esse sistema permite registrar um gráfico da corrente em um circuito em função do tempo. Como parte do teste, v
50- Suponha que a espira da Figura 29.45 seja ( a ) girada em torno do eixo O y ( b ) girada em torno do eixo O x ( c ) girada em torno de um lado da espira paralelo ao eixo O z Qual é a fem induzida