Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.

Um múon (uma partícula elementar) penetra em uma região com uma velocidade de 5,00 × 10 6   m / s e passa a ser desacelerado a uma taxa de 1,25 × 10 14   m / s 2 . (a) Qual é a distância percorrida pelo múon até parar? (b) Desenhe os gráficos de x em função de t e v em função de t para o múon.

Passo 1

Galera, vamos usar a equação de Torricelli para encontrar a distância percorrida.

v 2 = v 0 2 + 2 a Δ x → Δ x = v 2 - v 0 2 2 a = 0 2 m / s - 5,00 × 10 6 m / s 2 2 . - 1,25 × 10 14   m / s 2  

Δ x = 10,0   c m

Passo 2

A posição x em termos de t   é dada pela função horária da posição:

x = x 0 + v 0 t + a t 2 2

x = 0 + 5,00 × 10 6 . t + - 1,25 × 10 14 2 . t 2

x = 5,00 × 10 6 . t - 6,25 × 10 13 . t 2

Passo 3

A velocidade é em relação ao tempo é dada pela função horária da velocidade.

v = v 0 + a t

v = 5,00 × 10 6 - 1,25 × 10 14 . t

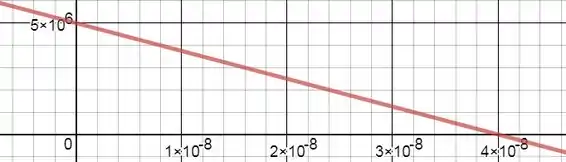
Resposta

a)   Δ x = 10,0   c m

Ver Outros Exercícios desse livro