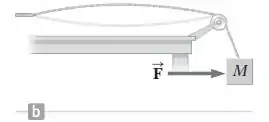
Considere o aparelho mostrado na Figura P14.68a, onde o corpo pendurado tem massa M e a corda vibra em seu segundo harmônico. A lâmina vibratória na esquerda mantém frequência constante. O vento começa a soprar para a direita, aplicando uma força horizontal constante F no corpo pendurado. Qual é a intensidade da força que o vento deve aplicar sobre o corpo pendurado de modo que a corda vibre em seu primeiro harmônico, como mostra a Figura 14.68b?
Passo 1
Fala ai galera, bora resolver o nosso exercício? Se liga só.
Para a gente resolver o nosso exercício, primeiro temos que focar na figura P14.68a :

Nesse caso, o nosso Bloco se encontra em equilíbrio. Ou seja, a tensão que a corda exerce segurando o bloco é igual a força peso do mesmo, que puxa ele para baixo:
Além disso, como estamos trabalhando com uma corda, vamos usar a fórmula:
Vamos dizer aqui que pois é uma onda inteira por comprimento da mesa
Juntando a equação (1) e a (2):
Passo 2
Beleza, agora vamos olhar para o segundo caso, para a figura P14.68b :
Vamos dar um zoom aqui na região do bloco com a tensão da corda:
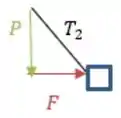
Reparem que temos aqui um triângulo retângulo, então vamos usar Pitágoras:
Show, agora reparem que o comprimento da mesa (L) vai ser metade do comprimento de onda, ou seja, . Vamos usar as mesmas fórmulas do Passo 1:
Elevando os dois lados ao quadrado, vamos ter:
Passo 3
Beleza galera, conseguimos definir as fórmulas para cada caso, para acharmos a força necessária, vamos usar a equação (3) do Passo 1 e a equação (4) do Passo 2:
Vamos dividir a equação (4) pela (3):
Vamos começar a simplificar:
Elevando os dois lados ao quadrado:
Tirando a raiz de cada lado: