(a) Considere que a definição do coeficiente de expansão volumétrico seja:
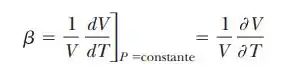
Use a equação de estado para um gás ideal para mostrar que o coeficiente de expansão volumétrica para um gás ideal sob pressão constante é dado por , onde é a temperatura absoluta. (b) Que valor esta expressão prevê para a ? Diga como esse resultado é comparado com os valores experimentais para (c) hélio e (d) ar na Tabela 16.1. Observação: Estes valores são muito maiores que os coeficientes de expansão volumétrica para a maioria dos líquidos e sólidos.
Passo 1
Falaaaaaaaaaaaaaaaa Tribuxo?
Bora resolver mais uma questão!?
Vamos para resolver esse exercício faremos:
Como estamos derivando e considerando um gás ideal, podemos escrever:
Isolando :
Podemos substituir na primeira equação:
Realizando a derivada:
Se voltarmos na equação do gás ideal, podemos isolar
Se elevarmos a :
Podemos substituir em :
Passo 2
(a) Temos pelo passo acima:
Passo 3
(b)Substituindo temos:
Passo 4
(c) Iremos fazer:
Passo 5
(d) Iremos fazer:
Mandamos bem nessa!!!!!!
Até a próxima questão..............