Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 3.1 - Ex. 7
Considere dois deslocamentos, um de módulo 3 m e outro de módulo 4 m. Mostre de que forma os vetores deslocamento podem ser combinados para que o módulo do deslocamento resultante seja (a) 7 m, (b) 1 m, (c) 5 m.
Passo 1
Faala ae, beleza?? Aqui, temos dois deslocamentos, ou seja, dois módulos de vetores, que vamos chamar de e . Com isso, nossas informações são:
Beleza? E a questão pede o módulo do vetor resultante desses dois deslocamentos. Vamos chamar esse vetor resultante de , ok?
Para isso, lembraremos que o módulo do vetor resultante é dado pela Lei dos Cossenos:
Onde é o ângulo entre esses dois vetores e .
Passo 2
(a) Então, vamos lá! Primeiro, queremos que . Substituindo isso na fórmula do passo anterior:
Fazendo as contas, isolando o :
Para que o cosseno seja , temos que o único ângulo possível para gente é o . Portanto, se o ângulo entre os vetores deslocamentos é , esses vetores podem ser escritos assim:
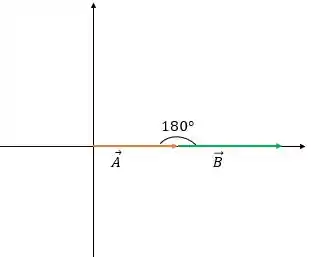
Passo 3
(b) Agora, queremos que . Substituindo isso na fórmula do passo anterior:
Fazendo as contas, isolando o :
Para que o cosseno seja , temos que o único ângulo possível para gente é o . Portanto, se o ângulo entre os vetores deslocamentos é , esses vetores podem ser escritos assim:
Passo 4
(c) Queremos que . Substituindo isso na fórmula do passo anterior:
Fazendo as contas, isolando o :
Para que o cosseno seja , temos que o ângulo pode ser ou . Portanto, se o ângulo entre os vetores deslocamentos é , esses vetores podem ser escritos assim:
E, se for :
Beleza?? Acabou! Só isso! 😊
Resposta
(a) entre os vetores.
(b)
(c) ou entre os vetores.