Considere a máquina do ciclo Brayton (Problema 83) funcionando ao contrário, como refrigerador, em sua cozinha. Nesse caso, o ciclo inicia à temperatura e se expande a pressão constante até sua temperatura . O gás é, então, comprimido adiabaticamente, até que sua temperatura seja . Depois, ele é comprimido à pressão constante até a sua temperatura . Finalmente, ele se expande adiabaticamente até retornar ao seu estado original à temperatura .
- Esboce este ciclo em um diagrama PV.
- Mostre que o coeficiente de desempenho é
- Suponha seu "refrigerador em ciclo Brayton" funcionando da seguinte maneira. O cilindro contendo o refrigerante (um gás monatômico) tem um volume e uma pressão iniciais de 60 mL e 1,0 atm. Depois da expansão a pressão constante, o volume e a temperatura são de 75 mL e –25 ° C. A relação de pressão para o ciclo é de 5,0. Qual é o coeficiente de desempenho do seu refrigerador?
- Para absorver o calor do compartimento de alimentos a taxa de 120 W, qual é a taxa na qual deve ser fornecida energia elétrica para o motor do refrigerador?
- Supondo que o motor do refrigerador funcione efetivamente por apenas 4,0 h por dia, quanto ele acrescenta à sua conta mensal de energia elétrica? Suponha 15 centavos por kWh de energia elétrica e trinta dias em um mês.
Passo 1
Bom, queremos o diagrama do ciclo de Brayton. Que é composto de:
- Expansão isobárica: há um aumento do volume mantendo a pressão constante, e removendo calor no ciclo da fonte fria;
- Compressão adiabática: neste caso não há troca de calor, o volume está diminuindo e aumentando a pressão;
- Compressão isobárica: há diminuição do volume mantendo a pressão constante, liberando calor para a fonte quente;
- Expansão adiabática: não há troca de calor, o volume está aumentando e a pressão diminuindo.
Desenhando o ciclo:
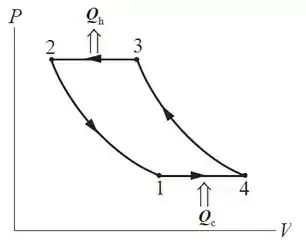
Essa até que foi fácil! Vamos continuar!
Passo 2
O coeficiente de desempenho para um refrigerador é calculado como:
Sabemos que:
Então:
Como o calor é o calor absorvido do processo 14, , temos:
Como temos um processo à pressão constante, podemos calculá-lo como:
Já o calor é o calor liberado durante o processo 23, então:
Como temos um processo à pressão constante, podemos calculá-lo como:
Substituindo na eficiência:
Reorganizando:
Passo 3
Muito bem, para achar CD precisamos de todas as temperaturas. Já sabemos que, depois do processo de expansão adiabática, processo 14:
Como a pressão é constante de 14, pela lei dos gases ideais:
O termo é constante para os pontos 1 e 4:
Sabendo que:
Substituindo:
O processo de 34 é adiabático, então usamos a relação:
Isolando
Sabendo que:
Onde g são os graus de liberdade. Como o gás é monoatômico,
Se:
Substituindo:
A mesma relação pode ser usada para o processo 12:
Então:
Substituindo:
Na fórmula do passo 2:
Terminamos mais uma !
Passo 4
Na letra d queremos a taxa na qual deve ser fornecida energia elétrica, ou seja, a potência. E o que é a potência:
Não temos o trabalho, então devemos calculá-la de forma diferente. Vamos usar o coeficiente de desempenho para isso.
No caso dos refrigeradores:
Se queremos a variação pelo tempo:
Modificando um pouco mais, a variação do trabalho pelo tempo pode ser calculada simplesmente como:
Onde f é a frequência, dada em . O calor à pressão constante pode ser calculado como:
Lembrando que
Vamos substituir na equação do trabalho pelo tempo:
Bem, agora o que temos?
Ninguém nos disse nada sobre a frequência, mas vamos analisar esta potência durante um intervalo de um minuto, ok?
Só não temos como dizer nada sobre os mols, mas temos tudo o que precisamos para calculá-lo.
Se vocês lembrarem da lei dos gases ideais:
Temos todos os dados que precisamos para calcular no ponto 4, certo? Então bora usá-lo:
Substituindo:
Colocando os dados:
Passo 5
Queremos saber quanto de energia esse refrigerador funcionando 4,0 h por dia e trinta dias em um mês, suponha 15 centavos por kWh de energia elétrica.
Já sabemos que o refrigerador consome 0,207 kWh. Então:
Passo 6
- -
- -
Resposta
Ei, a resposta está no passo a passo :)