Considere uma partícula se movendo em um potencial desenhado na figura 5-22.
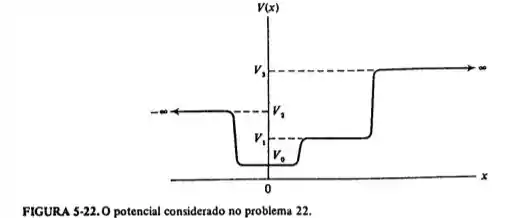
Para os seguintes intervalos de valores da energia total , diga quando há algum valor possível de E, e, se isto ocorre, se eles são separados discretamente ou distribuídos continuamente. (a) , (b) , (c) , (d) , (e) .
Passo 1
Fala galerinha, beleza?
O enunciado apresenta um erro no item (e). A expressão correta é .
Primeiro vamos representar os níveis de energia de cada item no diagrama:
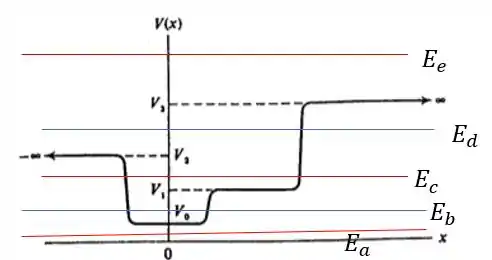
Como os valores de energia devem sempre ser maiores que o mínimo do potencial, não é possível. Os demais valores de energia são todos possíveis!
Passo 2
Para que os níveis de energia sejam discretizados, a energia deve ser tal que classicamente a partícula fique “presa”. Isso só ocorre para e . Observe que para , a partícula está limitada com relação a seu movimento para direita, mas o movimento para a esquerda é ilimitado por e conforme . Por fim, para o movimento é ilimitado nas duas direções, de modo que a energia é contínua, assim como para .
Resposta
Impossível: (a)
Discreto: (b) e (c)
Contínuo: (d) e (e)