Um corpo de massa igual a 4 kg move-se para cima num plano inclinado de 20 graus com a horizontal. As seguintes forças agem sobre o corpo: uma força horizontal de 80 N, uma força de 100N paralela ao plano inclinado no sentido do movimento, e uma força de atrito constante de 10 N que se opõe ao movimento. O corpo desliza 20 m sobre o plano. Calcule o trabalho total realizado pelo sistema de forças que age sobre o corpo, assim como o trabalho executado por cada uma delas.
Passo 1
Fala galeraa, tudo bem??
Vamos relembrar um pouquinho de trabalho?? O trabalho é uma grandeza física que mede a transferência de energia e é dado pela transferência de força ao longo de um deslocamento. Assim, podemos dizer que o trabalho pode ser dado pelo produto escalar entre o deslocamento e a força realizada. Ou seja:
Passo 2
Além disso, vamos entender o que ocorre neste caso descrito pelo enunciado.
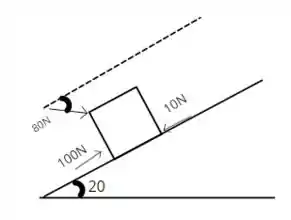
Pensando desta forma, teremos 3 forças agindo no bloco e formando a força resultante. Teremos a força de 100N, a de -10 N e a de 80N, que precisaremos decompor em Fx. Ou seja, teremos que:
F1= 100N
F2= -10N
F3= 80*cos𝜽= 80*cos(20)N
Logo, a força resultante será:
Fr = 100 - 10 + 80 * cos (20)
Fr = 165,2 N
Passo 3
Voltando ao trabalho, então, temos que:
, com F=165,2N e o deslocamento de 20m
Logo, encontramos que o trabalho total foi de 3.304 J.
Passo 4
Agora, vamos calcular o trabalho em cada um dos casos, com F1, F2 e F3. Teremos,
para F1:
Para F2:
Para F3: