Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 34.Exercícios e Problemas - Ex. 70

A corrente através de uma indutância L é dada por I =   I 0 e - t τ     .

  1. Obtenha uma expressão para a diferença de potencial Δ V L através do indutor.
  2. Calcule Δ V L nos instantes t = 0 ,   1 ,   2   e   3 m s para o caso em que   L = 20   m H ,       I 0 = 50   m A   e τ =   1,0   m s .  
  3. Desenhe o gráfico Δ V L versus tempo desde t =   0   s até t =   3   m s

Passo 1

Faaaaaala, galera... Tranquileba??

Para a)

Sabemos que:

V L = - L d I d t

Dado que:

I = I 0 e - t τ

Assim:

V L = - L d d t I 0 e - t τ

Logo:

V L = L I o τ e - t τ

Bora pro próximo item?!

Passo 2

Para b)

Para t = 0

V L = 20 ×   10 - 3 H 50 × 10 - 3 A 1.0 × 10 - 3   s

V L = 1 V

Para t = 1   m s

V L = 20 ×   10 - 3 H 50 × 10 - 3 A ( 1.0 × 10 - 3   s ) e - ( 1.0 × 10 - 3   s ) ( 1.0 × 10 - 3   s )

V L = 0.37 V

Para t = 2.0 m s

V L = 20 ×   10 - 3 H 50 × 10 - 3 A ( 1.0 × 10 - 3   s ) e - ( 2 . 0 × 10 - 3   s ) ( 1.0 × 10 - 3   s )

V L = 0.13 V

Para t = 3   m s

V L = 20 ×   10 - 3 H 50 × 10 - 3 A ( 1.0 × 10 - 3   s ) e - ( 3 . 0 × 10 - 3   s ) ( 1.0 × 10 - 3   s )

V L = 0.05   V

Passo 3

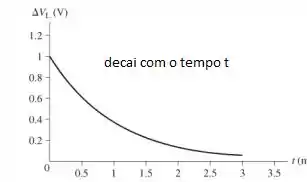
Para c)

Fazendo um gráfico disso, temos:

Resposta

Para a)

V L = L I o τ e - t τ

Para b)

Para t = 0

V L = 1 V

Para t = 1   m s

V L = 0.37 V

Para t = 2.0 m s

V L = 0.13 V

Para t = 3   m s

V L = 0.05   V

Para c)

Ver Outros Exercícios desse livro