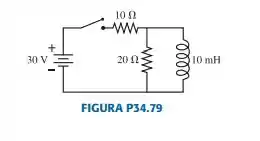
O interruptor da FIGURA P34.79 ficou aberto por um longo tempo. Ele é fechado em . Qual é a corrente através do resistor de
- Imediatamente após o interruptor ser fechado?
- Após o interruptor ter ficado fechado por um longo período de tempo?
- Imediatamente após o interruptor ser reaberto?
Passo 1
Faaaaaala, galera... Tranquileba??
Para a)
Podemos aplicar a lei das malhas de Kicrhhoff para a primeira e para a segunda malha.
Para a primeira malha:
Sendo:
Assim:
Para a segunda malha:
Analisando a equação da voltage em um condutor:
Há um principio que diz não há corrente em um condutor imediatamente após ele ser ligado, porque .
Logo toda a corrente será para a primeira malha.
Bora pro próximo passo?!
Passo 2
Para b)
A corrente através de um indutor cresce com o tempo. Uma vez que ele atinge uma corrente estável e não se altera mais, então ficando em “curto” com o resistor de . E desse modo a corrente da primeira malha passara pelo indutor também, logo ficando nula. Portanto:
Passo 3
Para c)
O indutor está em “curto” com o resistor de . Sendo a chave aberta depois de um longo tempo, a corrente passando pelo indutor e o resistor é de Por causa da corrente passar através não poder mudar instantaneamente, a corrente deve retornar a 3.0 imediatamente após a chave ser reaberta. Essa corrente deve ir a algum lugar (conservação de corrente), mas agora coma chave aberta prevê que a corrente retorne a bateria. Sendo assim, a corrente pelo resistor de é de
Resposta
Para a)
Para b)
Para c)