Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Mecânica- Ed: 2º - Capítulo 11.Problemas - Ex. 16

Demonstre que v c = 1 - m 0 c 2 E 2 1 2 .   A partir dessa relação calcule a velocidade de uma partícula, quando E é (a) igual à sua energia de repouso, (b) duas vezes a sua energia de repouso, (c) 10 vezes a sua energia de repouso e (d) mil vezes a sua energia de repouso. Calcule as energias correspondentes, em e V , para um elétron e um próton. Faça um gráfico de v / c contra E / m 0 c 2 .

Passo 1

E aí, beleza?? Podemos relacionar a velocidade com a energia com:

E 2 = m 0 c 2 2 + p c 2 ∴ p c = E 2 - m 0 c 2 2

Ou seja:

p c E = γ m v c γ m c 2 = v c = 1 - m 0 c 2 E 2 1 2

Portanto:

v c = 1 - m 0 c 2 E 2 1 2

Como queríamos demonstrar.

Passo 2

Para os itens, temos:

  1. β = 0
  2. β = 0,87
  3. β = 0 , 995
  4. β = 0 , 9999995

Passo 3

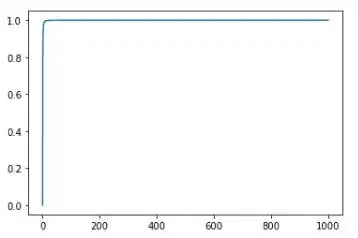
Assim, o gráfico de β por E / E 0 é:

Resposta

  1. β = 0
  2. β = 0,87
  3. β = 0,995
  4. β = 0,9999995
Ver Outros Exercícios desse livro