Deseja-se encostar uma tabua de comprimento e massa formando um ângulo com
a parede. Se o coeficiente de atrito estático entre a tabua e o chão for e supondo que não exista atrito entre a tábua e a parede, qual deve ser o angulo para que a tábua se mantenha em equilíbrio estático?
A forca peso está aplicada no centro da tábua.
Passo 1
O primeiro elaborar um DCL, esquematizando as forças atuantes em cada ponto do sistema:
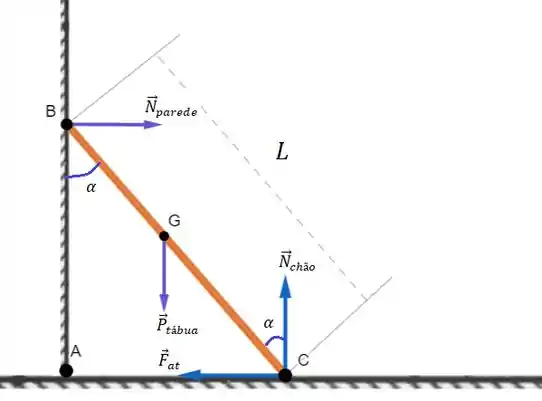
Passo 2
Para a tábua permanecer estática ou em equilíbrio estático:
Aplicando as condições de equilíbrio, podemos deduzir nossas equações:
Passo 3
Vamos começar pelas forças em :
Mas:
Subst. na equação:
Passo 4
Em :
Porém sabemos que:
Subst. temos que:
Passo 5
Vamos agora calcular o torque no ponto , adotando como positivo o sentido anti-horário.
O torque no ponto é gerado apenas pelo peso da tábua, e pela força normal de reação ao apoio na parede:
Vamos determinar as distâncias perpendiculares a linha de ação de cada uma das duas forças em relação ao ponto de rotação
: Como a centro de massa da tábua está localizado no centro da tábua, então a distância perpendicular da linha de ação da força ao ponto de rotação , é a metade de :
Usamos o triângulo para determinar a distância :
Como o que queremos é :
Para a força : A distância perpendicular da linha de ação da força até o ponto , é
Semelhante a podemos determinar :
Agora podemos determinar o torque:
Passo 6
Simplificando dos dois lados, temos:
Subst.
simplificando , temos:
Resposta