Enunciado
Física - Cutnell e Johnson - Física- Ed: 9º - Capítulo 4.Problemas - Ex. 28
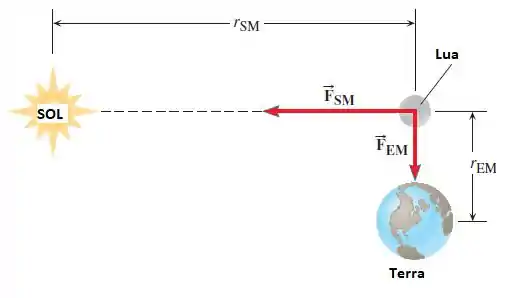
O desenho abaixo (fora de escala) mostra um alinhamento do sol, terra e lua. A força gravitacional que o sol exerce na lua é perpendicular a força que a terra exerce na lua. As massas são: massa do sol = , massa da terra = , massa da lua = . As distâncias mostradas no desenho são e . Determine a magnitude da força gravitacional resultante na lua.
Passo 1
Bora que bora desenrolar esse paranauê aí? Então, a magnitude da força resultante atuando na lua pode ser encontrada como?
Conseguimos observar que nossa força resultante que atua na lua tem uma componente na horizontal, e uma outra na vertical que é . Portanto, a magnitude da força que atua na lua deve ser dada por Pitágoras.
Passo 2
De acordo com a lei de gravitação de Newton, se aplicarmos em cada uma das forças que estão no nosso desenho, temos:
Onde G é a constante gravitacional, o subíndice “E”, “M” e “S” são relativos a terra, lua e sol, respectivamente.
Substituindo os valores nas equações acima a gente encontra os valores das nossas forças, certo?
Passo 3
Portanto, a magnitude da força que atua na lua é de: