Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Cutnell e Johnson - Física- Ed: 9º - Capítulo 4.Problemas - Ex. 29

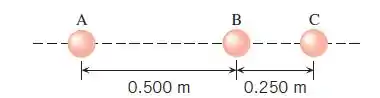
O desenho a seguir mostra três partículas distantes de qualquer outro objeto e localizadas em linha. As massas das três partículas A, B e C são 363 kg, 517 kg e 154 kg, respectivamente. Encontre a magnitude e direção da força gravitacional resultante atuando na (a) partícula A, (b) partícula B, e (c) partícula C.

Passo 1

E aí, galerinhaaa! Tranquilidade? Vamos que vamos para mais um problema de mecânica?

Vamos primeiro entender por conceitos o que precisamos fazer!!! Cada partícula experimenta duas forças gravitacionais, concorda? Onde cada força gravitacional vai estar relacionada com sua respectiva partícula. Para obter a força resultante gravitacional, nós precisamos adicionar as duas contribuições, porém lembrando das suas direções e sentido. A magnitude da força gravitacional que qualquer partícula exerce em outra é dada pela lei gravitacional de Newton.

F = G m 1 m 2 r 2

Passo 2

Então vamos calcular a força gravitacional de cada PAR de partícula:

F A B = G m A m B r 2 = 6,67 × 10 - 11 363 517 0,5 2 = 5,007 × 10 - 5 N

F B C = G m B m C r 2 = 6,67 × 10 - 11 517 154 0,5 2 = 8,497 × 10 - 5 N

F A C = G m A m C r 2 = 6,67 × 10 - 11 363 154 0,5 2 = 6,629 × 10 - 6 N

Passo 3

(a) Ambas partículas B e C atraem a partícula A para direita, a força resultante é:

F A = F A B + F A C = 5,007 × 10 - 5 + 6,629 × 10 - 6 = 5,67 × 10 - 5 ,   d i r e i t a

(b) Partícula C atrai a partícula B para esquerda, enquanto a partícula A atrai para direta, logo:

F B = F B C - F A B = 3,49 × 10 - 5   d i r e i t a

(c) A partícula A e B atraem a partícula C para esquerda, logo:

F C = F A C + F B C = 9,16 × 10 - 5   ( e s q u e r d a )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro