Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 30.Exercícios e Problemas - Ex. 76

Um detector de radiação conhecido como contador Geiger emprega um tubo cilíndrico fechado e oco com um fio isolante ao longo de seu eixo longitudinal. Suponha que um tubo de Geiger, como é chamado, contenha um fio de 1,0   m m de diâmetro em seu interior e tenha um diâmetro interno de 25   m m . O tubo é preenchido com um gás a baixa pressão com rigidez dielétrica de 1,0 ×   10 6 V m . Qual é a diferença de potencial máxima possível entre o tubo e o fio?

Passo 1

Faaaaaala, galera... Tranquileba??

Primeiro precisamos saber qual o campo elétrico para um fio longo. Assim, usando a própria informação do livro:

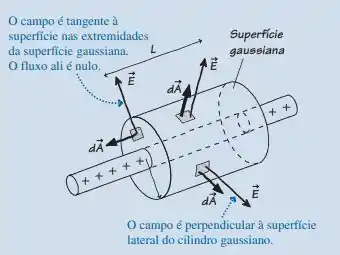
Dado que o campo é perpendicular a superfície e tomando a simetria do sistema podemos aplica a lei de Gauss para o fluxo Elétrico:

∮ E → ∙ d   A →   = Q i n t ε 0      

Sendo o campo constante em todo o fio, logo:

E * A = Q i n t ε 0

E a área gaussiana do fio é dada como:

A f i o = 2 π r L

E a densidade linear de carga é:

λ = Q L → Q = λ L

Assim ficando:

E = λ 2 π r   ε 0

E para relacionar o cmapo elétrico à diferença de potencial:

E = ∇ V

Assim, vamos ao segundo passo. Cola comigo

Passo 2

Assim:

Δ V = - ∮ E * d r

É pedido pra gente calcular a ddp do fio ao cubo, ou seja 25 m m ≤ r ≤ 1   m m . Assim:

Δ V = - ∮ 25 m m 1 m m λ 2 π r   ε 0 d r = - λ 2 π   ε 0 ln ⁡ ( r ) 1 m m 25   m m = λ 2 π   ε 0   l n ⁡ ( 25 )

Passo 3

Precisamos definir o valor e λ ,   para sabermos o modulo completo ddp. Assim, peguemos o campo máximo, ou seja, quando o raio é o menor possível, isto é r = 1.0   m m

E m á x i m o = λ m á x i m o 2 π ( 1.0 × 10 - 3 m )   ε 0 = 1 × 10 6 V m

Assim temos que:

λ m á x i m a = 2000   π   ε 0  

Assim, a diferença de potencial ddp pé:

Δ V = 2000   π   ε 0   2 π   ε 0 ln ⁡ 25 = 3.2 × 10 3 V = 3.2   k V

Resposta

Δ V = 3.2   k V

Ver Outros Exercícios desse livro