Determine as coordenadas do centro de massa do corpo homogêneo representado na Fig.4.44; , , , ,,
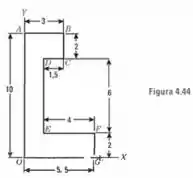
Passo 1
E aí, beleza?? Podemos dividir esse corpo em três retângulos e, a partir deles, determinar o centro de massa da figura completa. Ele será uma média ponderada dos centros de massa de cada retângulo, em que os pesos da média ponderada serão suas áreas. Assim, considere a seguinte figura:
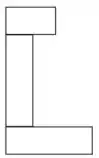
Essa será a divisão feita.
Passo 2
Assim, os centros de massa de cada retângulo, de baixo pra cima, são:
E as áreas são:
Portanto:
Assim: