Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Mecânica- Ed: 2º - Capítulo 10.Problemas - Ex. 33

Determine, para o sistema ela Fig. 10.39, a velocidade angular do disco e a velocidade linear de m e m'. Calcule a tensão em cada corda. Suponha quem= 600 g, m' = 500 g, M = 800 g, r = 8 cm e r = 6 cm.

Passo 1

Faala galera!! Aqui, vamos separar e organizar para entendermos melhor:

Movimento do disco:

T = I a ;   I = 1 / 2   M R ²   e   T = T R - T r '

Colocando na equação:

T R - T r ' = 1 / 2 M R ² a

Passo 2

Agora, vamos entender o diagrama de corpo livre abaixo:

m g - T = m Q

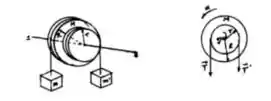
No movimento de m’ teremos:

T ' - m ' g = m ' a '

A partir da substituição das equações de cada um dos elementos da equação, nós temos que:

a = [ ( g / r ) * m - m ' ( r / R ) ] / [ ( M / 2 ) + m + m ' ( r / R ) ² ] = [ g / R * ( 600 - 500 * ( 3 / 4 ) ] / [ 400 + 600 + 500 * ( 9 / 16 ) ]

Logo, temos que:

a = ( 36 / 205 )   g / R ,   c o m o   R = 0,08 ,   l o g o ,   a = 21,55   R a d / s ²

Assim, teremos que:

a = R a ' = 36 R / 205 = 1,723   m / s ²

a ' = R a = ( 36 / 105 ) * ( 3 / 4 ) g = 1,292   m / s ²

Resposta

α = 21,55   R a d / s ² ,   a = 1,723   m / s ²

a ' = 1,292   m / s ²

Ver Outros Exercícios desse livro