Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Oscilações, Ondas e Termodinâmica- Ed: 5º - Capítulo 17.Problemas - Ex. 25

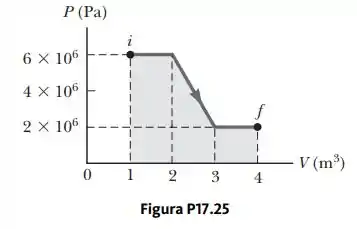
(a) Determine o trabalho realizado sobre um gás que se expande de i para f como indicado na Figura P17.25. (b) E se? Quanto trabalho é realizado sobre o gás se ele é comprimido de f para i ao longo da mesma trajetória?

Passo 1

Falaaaaaaaaaaaaaaaa Tribuxo?

Bora resolver mais uma questão!?

Temos:

W = - ∫ V i V f P d V

Para esse exercício vamos considerar a área do gráfico como nosso trabalho:

W = A

Sendo:

A t r i â n g u l o = 1 2 b h

A r e t â n g u l o = b h

No nosso caso:

A t r i â n g u l o = 1 2 P V

A r e t â n g u l o = P V

Para achar o trabalho de i → f , acharemos o trabalho por partes:

P a r t e   1 = P = 0 → 6 × 10 6   P a V = 1 → 2   m 3

P a r t e   2 = P = 2 × 10 6 → 6 × 10 6   P a V = 2 → 3   m 3

P a r t e   3 = P = 0 → 2 × 10 6   P a V = 2 → 4   m 3

Para:

P a r t e   1 :   W = - P V

P a r t e   2 :   W = - 1 2 P V

P a r t e   3 :   W = - P V

O trabalho se dará pelo somatório das partes:

W = W 1 + W 2 + W 3

W = - P 1 V 1 - 1 2 P 2 V 2 - P 3 V 3

Passo 2

(a) Substituindo:

W = 6 × 10 6 - 0 ⋅ 2 - 1 - 1 2 ⋅ 6 × 10 6 - 2 × 10 6 ⋅ 3 - 2 - 2 × 10 6 - 0 ⋅ 4 - 2

W = - 12 × 10 6   J

Passo 3

(b) Agora estamos invertendo, queremos de f → i , então:

W i → f = - W f → i

W f → i = 12 × 10 6   J

Mandamos bem nessa!!!!!!

Até a próxima questão..............

Resposta

  1. W = - 12 × 10 6   J = - 12   M J
  2. W f → i = 12 × 10 6   J = 12   M J
Ver Outros Exercícios desse livro