Devido à saliência do problema 24 por ser pequena, uma boa aproximação para a menor energia possível da partícula pode ser obtida tomando-a como a soma da energia quando não há saliência com o valor esperado da energia potencial extra representada pela saliência, tomando a correspondente à ausência da saliência para o cálculo do valor esperado.

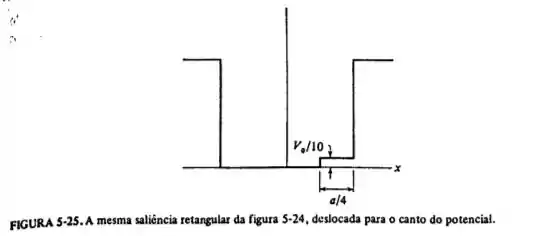
Usando esse ponto de vista, faça a previsão de se uma saliência do mesmo “tamanho”, mas localizada no canto do fundo, como na figura 5-25, teria um efeito igual, maior ou menor sobre a menor energia possível da partícula, comparado ao efeito da saliência no centro.

Fala galerinha, beleza?

Pelo que foi descrito no enunciado, uma aproximação para a energia do sistema é a energia sem a saliência somado ao valor esperado do potencial na região da saliência:

Para a saliência no centro (figura 5-24), temos

Já para a saliência na extremidade (figura 5-25):

É fácil perceber que é maior na região central do que no extremo, de modo que

Portanto, o efeito da saliência no extremo é menor do que no centro.