Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 88
Um dipolo elétrico que tem momento de dipolo está localizado a uma distância perpendicular de uma linha infinitamente longa de cargas que tem densidade linear uniforme . Considere que o momento de dipolo esteja na mesma direção e sentido do campo da linha de cargas. Determine uma expressão para a força elétrica no dipolo.
Passo 1
Veja a figura abaixo:
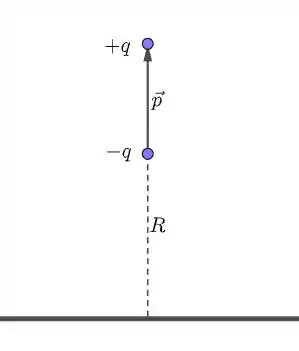
Vamos supor que o plano é positivamente carregado. Assim, temos que
onde é o módulo do campo elétrico atuando em e é o módulo do campo elétrico atuando em . Como
segue que
Assim,
Supondo que , temos
Passo 2
Finalmente, temos que
Resposta
A força é .
Exercícios de Livros Relacionados
78- Duas cargas puntiforme q 1 e q 2 são mantidas fixas a uma distância de 4.50c m . Outra carga puntiforme Q = - 1.75μ C , de massa igual a 5.0g , está inicialmente localizada a 3.0c m de cada uma de
Um pequeno objeto é solto no centro do capacitor da FIGURA Q27.14. Para cada situação descrita nos itens abaixo, o objeto se moverá para a direita, para a esquerda ou permanecerá no mesmo lugar? Se el
Nos Problemas de 62 a 65, uma ou várias equações lhe são fornecidas para a resolução de um problema. Em cada uma das questões, Elabore um problema realista para o qual o conjunto de equações fornecido
O dipolo elétrico permanente de uma molécula de água (H2O) tem módulo igual a 6,2 ×10 - 30C m . Qual é o torque máximo possível sobre uma molécula de água em presença de um campo elétrico de5,0 ×10 8