Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 33.Exercícios e Problemas - Ex. 10

A que distância sobre o eixo de uma espira de corrente o campo magnético tem a metade da intensidade de campo no centro da espira? Expresse sua resposta como um múltiplo de R.

Passo 1

Faaaaaala, galera... Tranquileba??

Seja uma espira ideal:

Então:

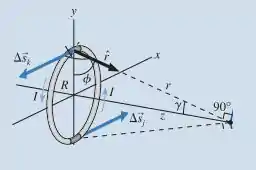
Vemos que as componentes em x e y se cancelam, sobrando somente em z.

Sabendo que a lei de bio-savart é:

B → = B x + B y + B z = 0 + 0 + B z = B cos ⁡ θ

d B = μ 0 4 π I   Δ s × r v e r s o r r 2 cos ⁡ θ

Veja que:

Δ s * r v e r s o r sin ⁡ 90 ° = 1 = Δ s

Assim:

d B = μ 0 4 π I Δ s r 2 cos ⁡ θ

E que:

r = R 2 + z 2

E também:

cos ⁡ θ = R r = R R 2 + z 2

Assim ficando:

d B = μ 0 4 π I Δ s R 2 + z 2   R R 2 + z 2 = μ 0 4 π I R   Δ s R 2 + z 2 3 2

Integrando sobre toda a espira:

B = μ 0 4 π I R R 2 + z 2 3 2 ∫ 0 2 π R Δ s = μ 0 4 π I R R 2 + z 2 3 2 2 π R

Concluímos que o campo magnético sobre uma espira é:

B e s p i r a = μ 0 2 I R 2 R 2 + z 2 3 2

Bora pro próximo passo!

Passo 2

Pede-se um ponto em z onde seja o dobro do campo em z = 0 , ou seja, 2 B 0 = B ( z )

Assim, faremos lado a lado. À esquerda, a uma distância z, e à direita, no ponto z = 0 . Assim:

μ 0 2 I R 2 R 2 + z 2 3 2 = 2 μ 0 2 I R

z 2 + R 2 3 2 = R 3 z

z 2 + R 2 = R 2 2 3 2

z = R 2 - 3 2 - 1 1 2

z = 0.77   R

Resposta

z = 0.77   R

Ver Outros Exercícios desse livro