Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 33.Exercícios e Problemas - Ex. 9
A que distâncias de um fio fino e reto, pelo qual flui uma corrente de 10 A, as intensidades de campo magnético são iguais às da Tabela 33.1?
Passo 1
Faaaaaala, galera... Tranquileba??
Sabemos que a lei de Bio-Savart é:
E para um fio muito longo, como:
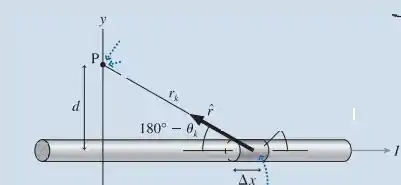
Temos que:
E:
Assim:
Sendo um fio muito longo, logo:
Logo:
De integral simples. Assim, o campo elétrico a uma distancia d sobre um fio longo que passa uma corrente é:
E tabela citada é:
Com esse “insight” nem precisa mais de mim, né?! Mas se gosta de mim, cola pro próximo passo!
Passo 2
Gostou né?! huehue
Brincadeiras à parte, pede-se d, então:
Sabemos que:
Passo 3
Para a superfície da terra:
Para o imã refrigerador:
Para o imã de laboratório:
E finalmente, o imã supercondutor:
Resposta
Para a superfície da terra:
Para o imã refrigerador:
Para o imã de laboratório:
E finalmente, o imã supercondutor: