Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Oscilações, Ondas e Termodinâmica- Ed: 5º - Capítulo 14.Problemas - Ex. 4

Dois alto-falantes idênticos são colocados em uma parede a 2,00 m um do outro. Um ouvinte está a 3,00 m da parede diretamente em frente a um deles. Um único oscilador impulsiona os alto-falantes a uma frequência de 300 Hz. (a) Qual é a diferença de fase em radianos entre as ondas dos alto-falantes quando alcançam o observador? (b) E se? Qual é a frequência mais próxima de 300 Hz para a qual o oscilador pode ser ajustado para que o observador ouça o som mínimo?

Passo 1

Bora bora boraaaaaaa, Cêis tão bonzinho??

Encoxxtaa comigoo

Antes de iniciarmos os cálculos, é importante lembrar que a diferença de fase é a diferença angular ou temporal entre duas ondas analisadas em um mesmo instante.

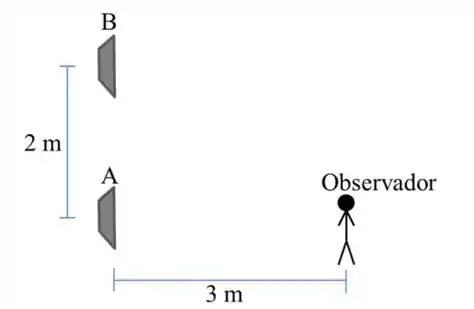
De acordo com a ilustração a seguir, as distâncias entre os alto-falantes ( r A / B )   e entre os alto-falantes e o observador ( r A   e   r B ) são:

Passo 2

r A = 3 m

r A / B = 2   m

r B = r A 2 + ( r A / B ) 2

r B = 3   m 2 + 2 m 2

r B = 9 m 2 + 2 m 2

r B = 3,6   m

∆ r = r B - r A

∆ r = 3.6 m - 3 m

∆ r = 0.6   m

Passo 3

  1. Para encontrarmos a diferença ade fase, é necessário, primeiramente, calcular o comprimento de onda

    2. λ = v f

    λ = 343 m s 300   H z

    λ = 1.14   m

    Passo 4

    Então, a defasagem de onda será:

    ∆ x λ = 0.6 1.14

    ∆ x λ = 0.526

    Convertendo em radianos

    ∆ ϕ = 2 π 0,526

    ∆ ϕ = 3,3   r a d

    Portanto, a diferença de fase entre as ondas quando alcançam o observador é de 3,3 rad.

    Passo 5

  2. Para que tenhamos uma interferência destrutiva com a frequência mais próxima de 300 Hz, adotaremos:

∆ x λ = 0,5

0,5 = f ⋅ ∆ v

Onde ∆ x = 6 m

f = v 2 ∆ x

f = 343 m s 2 ⋅ 0.6 m

f = 286   H z .

Resposta

  1. Portanto, a diferença de fase entre as ondas quando alcançam o observador é de 3,3 rad.
  2. f = 286   H z .
Ver Outros Exercícios desse livro