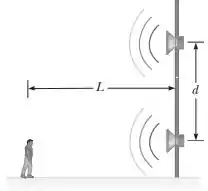
Dois alto-falantes idênticos são forçados a vibrar pelo mesmo oscilador a uma frequência f. Eles estão localizados a uma distância d em relação um ao outro sobre um poste vertical. Um homem caminha em linha reta em direção ao mais baixo, e perpendicular em relação ao poste, como mostra a Figura P14.6. (a) Quantas vezes ele vai ouvir um mínimo de intensidade sonora? (b) A que distância ele está do poste nesses momentos? Considere que v representa a velocidade do som e que o solo não reflete o som.
Passo 1
Alô Alô belezinhaa ??
Só vamoo??
Suponhamos que o homem esteja com os ouvidos no nível do alto-falante de baixo.
O som do alto-falante de cima está em atraso de fase devido à distância extra entre ele e o observador
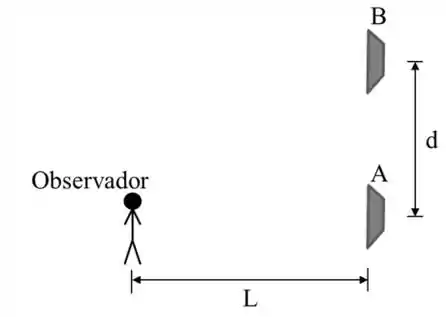
A distância entre o observador é:
A diferença de distância entre os alto-falantes e o observador é de .
O observador escuta o mínimo som quando , para
Igualando as duas equações de definidas anteriormente, temos:
Elevando toda equação ao quadrado, temos:
Passo 2
A equação (1) nos dá a distância entre o observador e o alto-falante mais próximo, onde ele escutará o mínimo.
- O número de vezes que o homem escutará o mínimo é o maior valor inteiro para , ou seja, a maior solução inteira para
- A equação (1) nos mostras distância em que o observador escutará o som mínimo. Então, para
Portanto, o número de mínimo escutando será :
Passo 3
Resposta
Vide a explicação.