Os dois blocos ( e ) da Fig. 6-38 não estão ligados. O coeficiente de atrito estático entre os blocos é , mas não há atrito na superfície abaixo do bloco maior. Qual é o menor valor do módulo da força horizontal para o qual o bloco menor não escorrega para baixo ao longo do bloco maior?
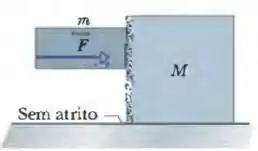
Passo 1
Vamos iniciar esta questão fazendo o diagrama do corpo livre para o bloco de massa e para o sistema formado pelos dois blocos:
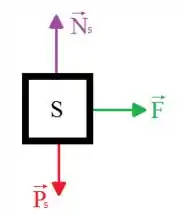
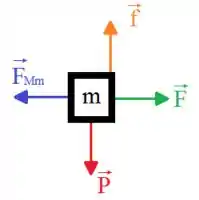
A partir da ilustração conseguimos visualizar melhor como as forças estão agindo sobre os blocos e assim facilita a aplicação da segunda lei de Newton.
Vamos aplicar a segunda lei de Newton ao eixo no sistema formado pelos dois blocos:
Agora, vamos aplicar a segunda lei de Newton aos eixos e do bloco de massa :
Foi considerado , pois o movimento ocorre exclusivamente no eixo e, vale lembrar também, que para esta questão estamos tratando de , pois desejamos o menor valor da força para que não deslize, ou seja, o bloco deve estar na iminência do movimento.
Passo 2
Isolando na a aceleração :
E substituindo na :
Isolando :
Passo 3
Para determinar o valor de devemos usar a para definir o valor de . Assim:
Isolando :
Substituindo essa expressão na :