Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 30.Exercícios e Problemas - Ex. 69
Dois capacitores e são carregados até e, depois, desconectados da bateria sem que ocorra variação de carga nas placas dos capacitores. Os dois capacitores são, então, conectados em paralelo um com o outro, com a placa positiva de conectada à placa negativa de e vice-versa. Logo em seguida, qual é a carga e qual é a diferença de potencial através de cada capacitor?
Passo 1
Faaaaaala, galera... Tranquileba??
Parece confuso o que o enunciado passa né?! Mas saca só, eler quer dizer isso aqui:
Maaaaas primeiro vamos achar a carga que cada um dos capacitores leva contigo. Pela formula:
Para
E para
Assim, podemos fazer a figura do enunciado de forma bonita. E obtemos:
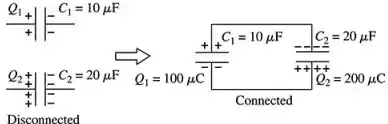
Passo 2
Após ambos serem conectados eles interagirão, formando assim:
Pela lei de Kirchhoff:
Assim:
Substituindo na nossa equação 0.1 a 0.2:
Logo
Passo 3
Como em ambos os capacitores a ddp é a mesma, peguemos por exemplo o primeiro: