Enunciado
Física - Cutnell e Johnson - Física- Ed: 9º - Capítulo 4.Cheque seu entendimentos - Ex. 10
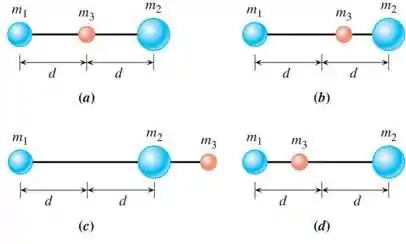
Dois objetos com massas e estão separados por uma distância . Sabemos que . Um terceiro objeto de massa é colocado em linha reta com os outros dois. Para que a força gravitacional resultante no objeto de massa seja zero, qual das configurações abaixo deve ser a correta?
Passo 1
Cheeegaaa maaaisss jooveeeem!! Bora acabar com todas e quaisquer dúvidas que você possa ter desse exerciociozinho aqui!!
Bom... a gente não consegue dar um passo sequer se não lembrarmos de como a força gravitacional é definida... lembra dela??
A formulinha deixa bem claro, olha só:
Ou seja, dois a dois, os corpos irão exercer influências um sobre o outro, e a magnitude dessa influência depende de nada mais do que das massas deles e da distância entre eles.
Passo 2
Bom... com isso em mente, para que o corpo 3 tenha força resultante zero.... elas precisam estar distribuídas de forma a se anularem.
Ou seja, a configuração (c) não pode ser a que procuramos pois as influências dos corpos 1 e 2 irão se somar no corpo 3
Vamos por partes... a força do objeto 1 sobre o 3 será:
E, naturalmente a força do objeto dois no terceiro:
Queremos que essas forças se anulem... ou seja:
Teremos:
Ta comigo até aqui?!
Passo 3
Agora, sabemos que a , então... vamos assumir que: , teremos:
E portanto:
Ou seja, a distância entre o objeto três e o dois...tem que ser maior do que a distância entre o três e o um.
Olhando matematicamente fica mais visível né?!
Em outras palavras, a única forma de as forças se anularem, sabendo que , é o objeto 3 estando o mais longe possível do objeto 2. Sacou??
A configuração que nos serve então, e a (d).
Pegou a ideia??
Chatinho, mas fácil! Bora pro próximo?! Te espero lá!!
Resposta
Portanto, a configuração (d) terá uma força gravitacional resultante igual a zero no objeto 3.