Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 32.1 - Ex. 65
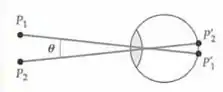
Se dois objetos puntiformes próximos entre si devem ser enxergados como dois objetos distintos, as imagens devem atingir a retina em dois cones diferentes que não sejam adjacentes. Isto é, deve haver um cone não ativado entre eles. A separação entre os cones é aproximadamente . Considere o olho como uma esfera uniforme de de diâmetro que tem índice de refração de . (a) Qual é o menor ângulo que os dois pontos podem formar? (Veja a figura abaixo). (b) Quão próximos os dois pontos podem estar se eles estão a do olho?
Passo 1
OPA, como você tá? Espero que bem, simbora resolver mais uma questão! Para resolvê-la usaremos a relação entre distância medida ao longo do arco de um circulo e o ângulo subtendido em seu centro para aproximar o menor ângulo que os dois pontos podem subtender e a separação dos dois pontos do olho. Pegou a visão (literalmente), então vamos resolver esse problema, baby!
Passo 2
Começaremos pela parte (a), relacionaremos ao diâmetro do olho e à distância entre os cones:
Substituindo as variáveis pelos valores numéricos e calculando :
Feito isto, vamos para a parte (b), acompanhe-me!
Passo 3
Na parte (b) deixaremos representar a separação dos pontos ao olho, para obter:
Prontinho, questão finalizada, fiquem bem, até a próxima, bons estudos, FUII!
Resposta
a)
b)