Duas bobinas idênticas são mutuamente paralelas e montadas sobre o mesmo eixo. Elas estão separadas por uma distância igual aos seus raios. Cada qual possui N espiras e conduz uma corrente de mesma intensidade e sentido que a outra.

1. Obtenha uma expressão para a densidade do campo magnético no ponto médio entre as espiras.
2. Calcule a intensidade do campo para espiras com 10 cm de diâmetro e 10 espiras conduzindo correntes de

Faaaaaala, galera... Tranquileba??

Bom, primeiro precisamos saber qual o campo elétrico a um ponto de distancia de uma espira, e em seguida aplicar à essa distancia o valor dado no enunciado. Confuso né, mas segue comigo!

Seja uma espira ideal:

Então:

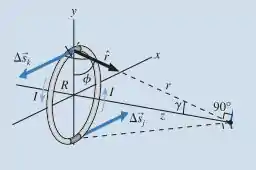
Vemos que as componentes em x e y se cancelam, sobrando somente em z.

Sabendo que a lei de bio-savart é:

Veja que:

Assim:

E que:

E também:

Assim ficando:

Integrando sobre toda a espira:

Concluímos que o campo magnético sobre uma espira é:

Agora aplicando a duas espiras:

E colocando z no centro entre ambas, ou seja, , temos:

Concluímos que:

Já foi dado a faca e o queijo né huehue