Enunciado
Física - Cutnell e Johnson - Física- Ed: 9º - Capítulo 1.Problemas - Ex. 52
Duas equipes de campo geológico estão trabalhando em uma área remota. Um global rastreador de sistema de posicionamento (GPS) em seu acampamento base mostra a localização de a primeira equipe a 38 km de distância, ao norte do oeste, e a segunda equipe a 29 km de distância, leste do norte. Quando a primeira equipe usa seu GPS para verificar a posição da segunda equipe, o que o GPS dá para a segunda (a) distância da equipe deles e (b) direção, medida a partir do leste?
Passo 1
Falaaaaaaaaaaaaaaaa Tribuxo?
Bora resolver mais uma questão!?
Vamos começar por algo divertido, o que acha????
Montando nosso diagrama, vamos pensar os caminhos do GPS, como se estivesse em um gráfico com eixos e , mas nosso será e será :
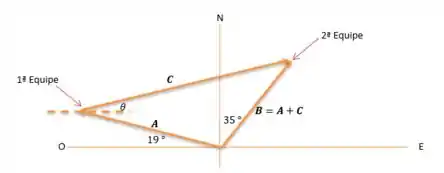
Ok, talvez não seja tão legal.
Passo 2
Teremos que a leitura da primeira equipe será:
Mas como sempre, a gente trabalha com componentes, então............................................
A gente precisa achar as componentes. Tá, mas como a gente acha as componentes, se liga só nisso:
Quando queremos achar quem está na componente , fazemos:
Se liga no macete, componente é cosseno, PORQUE.....................
E para :
Se liga no macete, componente é seno, PORQUE.....................
Pegou a dica???? é deitado (horizontal), e está de pé (vertical).
Teremos:
Passo 3
Para saber a distância, determinaremos a resultante:
Passo 4
Para saber a direção:
Foi divertido!!!!
Bora matar mais uma!