Enunciado
Física - Cutnell e Johnson - Física- Ed: 9º - Capítulo 1.Problemas - Ex. 55
Vector tem uma magnitude de 145 unidades e pontos 35° ao norte de Oeste. O vetor aponta 65° a leste do norte. Pontos do vetor 15° a oeste de Sul. Esses três vetores somados fornecem um vetor resultante que é zero. Usando componentes, encontre as magnitudes de (a) vetor é e (b) vetor .
Passo 1
Falaaaaaaaaaaaaaaaa Tribuxo?
Bora resolver mais uma questão!?
Vamos começar por algo divertido, o que acha????
Montando nosso diagrama, vamos pensar os caminhos do GPS, como se estivesse em um gráfico com eixos e .
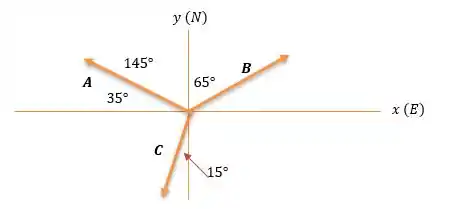
A gente precisa achar as componentes. Tá, mas como a gente acha as componentes, se liga só nisso:
Quando queremos achar quem está na componente , fazemos:
Se liga no macete, componente é cosseno, PORQUE.....................
E para :
Se liga no macete, componente é seno, PORQUE.....................
Pegou a dica???? é deitado (horizontal), e está de pé (vertical).
Passo 2
Para achar os valores de e , faremos:
Isolando :
Substituindo na segunda equação temos:
Multiplicando tudo por :
Aplicando :
Foi divertido!!!!
Bora matar mais uma!