Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 31
Duas forças de são aplicadas em cantos opostos de uma placa retangular, como mostrado na Figura 12-41. (a) Determine o torque produzido por este binário, usando a Equação 12-6. (b) Mostre que o resultado é o mesmo, se você determina o torque em relação ao canto esquerdo de baixo.
Passo 1
Olha aí como vai ficar o diagrama dessa parada:
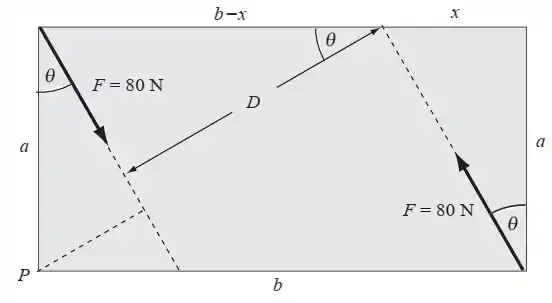
Passo 2
- A equação do binário que ele fala (da equação 12-6) é:
- Agora vamos calcular o torque em relação ao ponto inferior esquerdo, com relação a um eixo normal ao plano, pelo ponto P:
Desse diagrama, a gente vê que:
Juntando as uas:
Daí, o torque vai ser:
Substituindo valores numéricos:
Passo 3
Exatamente como encontramos na letra (a).
Resposta
Exercícios de Livros Relacionados
Um cubo homogêneo, de aresta a e massa M , está sobre uma superfície horizontal. Uma força horizontal F → é aplicada no topo do cubo, como mostrado na figura 12-42. Esta força não é suficiente para de