Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Campos e Ondas- Ed: 2º - Capítulo 14.Problemas - Ex. 60

Duas grandes placas de metal planas, montadas verticalmente e separadas por 4 cm, são carregadas com uma diferença de velocidade potencial de 200 V (a) Com que velocidade deveria ser lançada um elétron horizontalmente da placa positiva de modo que atinja a placa negativa com a velocidade de 107 m s-1? (b)

Passo 1

Opaaa tudo bem?

Vamos lá para mais um problema bem legal ein!

Passo 2

a. Fiz um desenho esquemático pra ficar mais fácil de a gente visualizar, beleza?

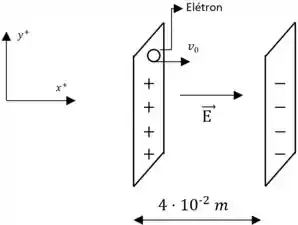
Passo 3

Temos a relação do movimento

v 1 2 - 2 a d = v 0 2 → v 0 = v 1 2 - 2 a d

A aceleração a é definida por

q E → = - e V d = m a → → a = - e V d m

Temos os dados então podemos substituir na expressão

a = - 1,6 ⋅ 10 - 19   C 200   V 4 ⋅ 10 - 2   m 9,091 ⋅ 10 - 31   k g → a = - 8,79 ⋅ 10 14   m / s 2

Podemos substituir o valor da aceleração a na equação para a velocidade inicial v 0

v 0 = v 1 2 - 2 a d = 10 7   m / s 2 - 2 - 8,79 ⋅ 10 14   m / s 2 4 ⋅ 10 - 2   m

→ v 0 = 1,30 ⋅ 10 7   m / s

Passo 4

b. Fiz um desenho esquemático pra gente entender melhor o que ta acontecendo, beleza?

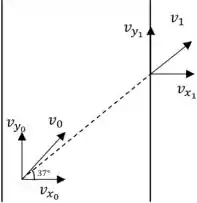
Podemos calcular de acordo com a equação do movimento

v x 1 2 = v x 0 2 + 2 a d = v 0 cos ⁡ 37 ° 2 + 2 a d

→ v 0 = v x 1 2 - 2 a d cos ⁡ 37 ° 2 = 10 7 m / s 2 - 2 - 8,79 ⋅ 10 14 m / s 2 4 ⋅ 10 - 2   m cos ⁡ 37 ° 2

→ v 0 = 1,63 ⋅ 10 7   m / s

Passo 5

c. A componente vertical de chegada é igual à componente vertical de saída

v y 1 = v y 0 = v 0 sin ⁡ 37 ° = 1,63 ⋅ 10 7 m / s ⋅ sin ⁡ 37 ° → v y 1 = 9,83 ⋅ 10 6   m / s

Passo 6

d. Vamos fazer para cada caso:

  • Para o caso a)

    • v 1 = v 0 + a t a → t a = v 1 - v 0 a = 1,30 ⋅ 10 7 m / s - 10 7 m / s - 8,79 ⋅ 10 14 m / s 2 → t a = 3,47 ⋅ 10 - 9 s

  • Para o caso b)

v x 1 = v x 0 + a t b → t b = v x 0 - v x 1 a = 1,63 cos ⁡ 31 °   m / s - 10 7   m / s - 8,79 ⋅ 10 14   m / s 2

→ t b = 7,21 ⋅ 10 14 s

Resposta

a. v 0 = 1,30 ⋅ 10 7   m / s

b. v 0 = 1,63 ⋅ 10 7   m / s

c. v y 1 = 9,83 ⋅ 10 6   m / s

d. t a = 3,47 ⋅ 10 - 9 s

t b = 7,21 ⋅ 10 14 s

Ver Outros Exercícios desse livro