Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Campos e Ondas- Ed: 2º - Capítulo 14.Problemas - Ex. 71

Temos um fio de comprimento L com densidade de carga linear λ (Fig. 14-51) (a) Prove que o campo elétrico em um ponto a uma distância R do fio é dado por

ε 1 = λ / 4 π ε 0 R sin ⁡ θ 2 - sin ⁡ θ 1

E

ε 2 = λ / 4 π ε 0 R cos ⁡ θ 1 - cos ⁡ θ 2

Onde ε 1 e ε 2 são os componentes de ε perpendicular e paralelo ao fio e θ 1 e θ 2 são os ângulos que formam as linhas traçadas do ponto às extremidades do fio com a perpendicular do ponto ao fio. ( b) Encontre o campo em um ponto equidistante das extremidades. (Os sinais dos ângulos θ 1 e θ 2 são indicados na figura).

Passo 1

Opaa tudo certo?

Vamos lá para mais um problema bem legal ein! Vou fazer a figura que ele dá no problema, beleza?

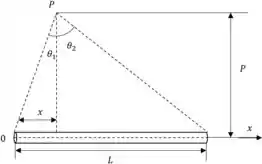
Passo 2

O esquemático para a solução é o seguinte

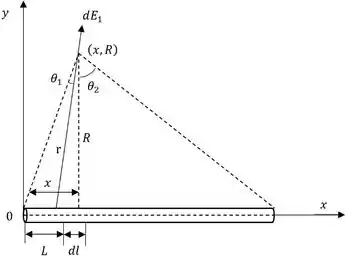
Passo 3

O campo elétrico é dado por

d E 1 = 1 4 π ε 0 ⋅ d q r 2

A carga é dada por

d q = λ d l

E a distância r é definida como

r = R 2 + x - 1 2

Passo 4

O campo elétrico então pode ser calculado por

d E = λ 4 π ε 0 ⋅ d l R 2 + x - 1 2 3 / 2

Integrando dos dois lados da equação, temos

E 1 = λ 4 π ε 0 ∫ 0 x l d l R 2 + x - 1 2 3 / 2 + ∫ 0 x R d l R 2 + x - 1 2 3 / 2

Vamos fazer o mesmo procedimento para E 2 .

Passo 5

O campo elétrico resultante é dado por

E = E 1 + E 2 = λ 4 π ε 0 cos ⁡ θ 1 - cos ⁡ θ 2 + sin ⁡ θ 1 - sin ⁡ θ 2

Passo 6

Quando o plano é paralelo temos que

E | | = λ 4 π ε 0 cos ⁡ θ 1 - cos ⁡ θ 2

Quando é perpendicular

E ⊥ = λ 4 π ε 0 sin ⁡ θ 2 - sin ⁡ θ 1

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro