Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 32.1 - Ex. 49
Duas lentes convergentes, cada uma com distância focal igual a , estão separadas por . Um objeto está a à esquerda da primeira lente. (a) Determine a posição da imagem final usando um diagrama de raios e a equação das lentes delgadas. (b) A imagem final é real ou virtual? A imagem final é direita ou invertida? (c) Qual é a ampliação lateral total?
Passo 1
(Música com direitos autorais tocando no fundo) EAE GALERA, nessa empolgação sonora, o clima é de resolver questão, não tem jeito! Para essa aplicaremos a equação das lentes delgadas para encontrar a imagem formada nas primeiras lentes e então usar essa imagem como objeto das segundas lentes. OK? Então vamo comigo, segue o baile, entra no clima!
Passo 2
Começando pela parte (a), vamos fazer um esboço de diagrama sobre como o sistema descrito na questão estaria, observem:
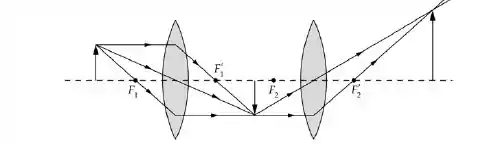
(Vocês não imaginam o trabalho que deu para conseguir essa imagem). Aplicando a equação das lentes delgadas para obter a distância da primeira imagem, temos:
Agora, encontraremos a ampliação lateral da primeira imagem:
Determinando essas propriedades da primeira imagem, poderemos ir para a segunda.
Passo 3
Por conta das lentes estarem separadas por , a distância do objeto para a segunda lente é de . Aplicando a equação das lentes delgadas, temos:
Então, a imagem final está a a direita do objeto; Agora, encontraremos a ampliação lateral da segunda imagem:
FEITA A LETRA (a). Agora, iremos para a letra (b).
Passo 4
(b) Por conta de , a imagem é real; Por conta de , a imagem é direita e duas vezes o tamanho do objeto. Para a parte (c) a ampliação lateral total é dada por .
QUESTÃO FINALIZADA COM SUCESSO.
Resposta
a) Posição da imagem final é a direita do objeto
b) Real e Direita
c)