Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 32.1 - Ex. 50

Repita o Problema 49, mas com a segunda lente substituída por uma lente divergente com distância focal igual a - 15   c m .

Passo 1

Queridos, hoje gera, utilizaremos literalmente o mesmo raciocínio do problema anterior, então, acompanhe-me os bons!

Passo 2

Começando pela parte (a), vamos fazer um esboço de diagrama sobre como o sistema descrito na questão estaria, observem:

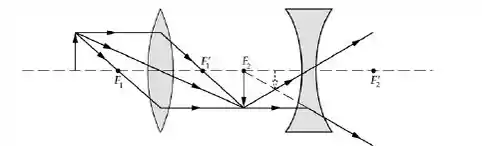
Aplicando a equação das lentes delgadas para obter a distância da primeira imagem, temos:

s 1 ' = f 1 s 1 s 1 - f 1

s 1 ' = 10   c m ( 20   c m ) 20   c m - ( 10   c m )

s 1 ' = 20   c m

Agora, encontraremos a ampliação lateral da primeira imagem:

m 1 = - s 1 ' s

m 1 = - 20   c m 20   c m

m 1 = - 1.0

Determinando essas propriedades da primeira imagem, poderemos ir para a segunda.

Passo 3

Por conta das lentes estarem separadas por 35   c m , a distância do objeto para a segunda lente é de 35   c m - 20   c m = 15   c m . Aplicando a equação das lentes delgadas, temos:

s 2 ' = f 2 s 2 s 2 - f 2

s 2 ' = - 15   c m ( 15   c m ) 15   c m - ( - 15   c m )

s 2 ' = - 7.5   c m

Então, a imagem final está a 48   c m a direita do objeto; Agora, encontraremos a ampliação lateral da segunda imagem:

m 2 = - s 2 ' s

m 2 = - - 7.5   c m 15   c m

m 2 = 0.50

FEITA A LETRA (a). Agora, iremos para a letra (b).

Passo 4

(b) Por conta de s ' 2 < 0 , a imagem é virtual; Por conta de m t o t a l = m 1 m 2 = - 0.50 , a imagem é invertida e metade do tamanho do objeto. Para a parte (c) a ampliação lateral total é dada por m t o t a l = m 1 m 2 = - 0.50 .

QUESTÃO FINALIZADA COM SUCESSO.

Resposta

a) Posição da imagem final é 48   c m a direita do objeto

b) Virtual e Invertida

c) m t o t a l = - 0.50

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você está trabalhando para um especialista em óptica durante o verão. Ele precisa medir uma distância focal desconhecida e você sugere usar o método de Bessel (veja o Problema 57), que você utilizou d
No método de Bessel para determinar a distância focal f de uma lente, um objeto e um anteparo estão separados por uma distância L , onde L4 f . É, então, possível, colocar uma lente entre o objeto e o
Uma lente convergente tem distância focal de 12.0c m . (a) Usando uma planilha eletrônica ou calculadora gráfica, faça um gráfico da distância imagem como função da distância objeto para distâncias ob
Se voce olhar no lado errado do telescopio,isto e,na objetiva,voce vera objetos distantes com tamanho angular reduzido. Para um telescopio de refracao que tem uma objetiva com distancia focal de 2,25
Qual eo poder de ampliacao de uma lente que tem uma distancia focal igual a 7,0 cm quando a imagemevista no infinito por uma pessoa cujo ponto proximo esta a 35 cm?